回到顶部 暗色模式

Leetcode题解（2）：二分搜索

原题地址: Problem 4
参考题解

        题目不用多解释，如果没有要求时间复杂度的话可以直接用双指针法遍历即可，但既然题目要求对数级的复杂度，再加上是排序数组，那么很容易就可以想到是二分法，接下来的问题就是怎么二分了。回忆下中位数的概念，中位数是一组顺序排序的数据中居于中间位置的数。也就是说，如果我们知道一组数据的中位数，我们就可以顺势以中位数为基准，将这组数据分成相同大小的两部分，其中一部分中的数总是小于（或等于）另一部分。再回到题目来，如果我们知道这两个数组的中位数，那么我们就可以将这两个数组以中位数为基准将每个数组分为两部分，如下所示：

将每个数组分为两部分, len1为nums1[]的长度，len2为nums2[]的长度

        其中左边两部分中所有的值永远小于或等于右边两部分。这时很明显中位数为

$$ median = \frac{max(nums1[i - 1], nums2[j - 1])\ +\ min(nums1[i] + nums2[j])}{2} $$

        这样我们的目标就从找中位数变成了寻找一个 $i$ 和 $j$ ，满足如下条件（假设 $i$ 和 $j$ 总是存在）：

  1.  $i + j = \Large\frac{nums1.length\ +\ nums2.length}{2}\normalsize;$
  2.  $nums1[i - 1] <= nums2[j];$
  3.  $nums2[j - 1] <= nums1[i].$

        根据上述条件，如果我们要进行二分搜索，第一步必须先将两个数组分别二分，保证条件1为真。

if (nums1.length > nums2.length) return findMedianSortedArrays(nums2, nums1);

int len1 = nums1.length,
    len2 = nums2.length,
    halfLen = (len1 + len2 + 1) / 2,
    i = len1 / 2,
    j = halfLen - i;
}

        可以发现我们在开始判断了下$nums1[\ \ ]$和$nums2[\ \ ]$的长度，确保 $nums1.length <= nums2.length$ 。这是因为我们在下面确定 $j$ 的值时，用到的赋值式是 $j = halfLen - i$ ，如果这时不满足 $nums1.length <= nums2.length$ 则会出现 $j$ 为非正的情况，因此要进行此判断。在计算 $halfLen$ 的时候，我们将 $Len1$ 和 $Len2$ 的和加一后再求平均值，目的也是保证 $halfLen - i > 0$ ，即 $j$ 为正数。
        经过上面的二分之后，我们得到了下图：

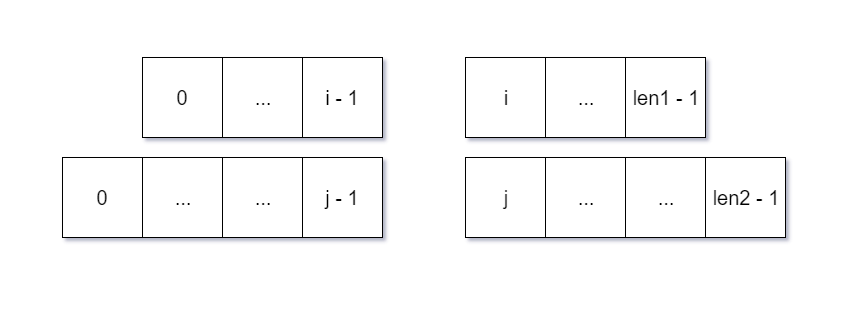
与上面的图片不同之处在于这幅图中左部分不一定小于等于右部分

        在得到了这幅图之后，有如下几种情况：

  1.  $nums1[i - 1] > nums2[j]$，即不满足条件2;
    • 说明 $i$ 过大，需要减小 $i$ 的值（增大 $j$ 的值）。
  2.  $nums2[j - 1] > nums1[i]$, 即不满足条件3;
    • 说明 $i$ 过小，需要增加 $i$ 的值（减小 $j$ 的值）。
  3.  $nums1[i - 1] <= nums2[j]$ 且 $nums2[j - 1] <= nums1[i]$，即满足条件2和条件3.
    • 说明找到了正确的 $i$ （和 $j$）。

        经过上面的整理之后，我们很容易就可以写出二分搜索过程中判断条件。

if (nums1.length > nums2.length) return findMedianSortedArrays(nums2, nums1);

int len1 = nums1.length,
    len2 = nums2.length,
    halfLen = (len1 + len2 + 1) / 2,
    iMin = 0,
    iMax = len1,
    i = 0,
    j = 0;

while(iMin <= iMax) {
    i = (iMin + iMax) / 2;
    j = halfLen - i;
    if (i > 0 && j < len2 && nums1[i - 1] > nums2[j]) iMax = i - 1;
    else if (j > 0 && i < len1 && nums2[j - 1] > nums1[i]) iMin = i + 1;
    else break;
}

        经过上面的搜索过程后，我们找到了正确的 $i$ 和 $j$，接下来要做的就只是特殊情况判断和返回值了。
        对于中位数的计算，我们可以通过两个变量分别记录左部分最大值和右部分最小值（如果需要的话），再取平均值。在此用 $left$ 记录左部分最大值，$right$ 记录右部分最小值。在非特殊情况下求 $left$ 的值只需要令 $left = Max(nums1[i - 1],\ nums2[j - 1])$ 即可。而这时显然对于左部分，会有两种特殊情况：

  1.  $i = 0$ ，说明 $nums1[\ \ ]$ 被全部划入右部分，这时显然 $left = nums2[j - 1]$ 。
  2.  $j = 0$ ，这时由于 $len1 <= len2$ ，所以当且仅当 $iMax = iMin = halfLen$ 即 $len1 = len2$ 时才会出现这种特殊情况，因此只需返回 $\Large\frac{nums1[i\ -\ 1]\ +\ nums2[j]}{2}$ 即可。

        在取得 $left$ 的值之后，如果 $len1 + len2$ 为奇数，则只需返回 $left$ 即可；若为偶数，则需要再处理 $right$。对于 $right$ ，同理有 $right = Min(nums1[i],\ nums2[j])$ ，也有两种特殊情况：

  1.  $i = len1$ ，说明 $nums1[\ ]$ 被全部划入左部分，这时显然 $right = nums2[j]$ 。
  2.  $j = len2$ ，当且仅当 $len1 = len2$ 时才会出现该情况，返回 $\Large\frac{nums1[i]\ +\ nums2[j\ -\ 1]}{2}$ 即可。

        将判断条件转化为代码即为：

int left = 0, right = 0;
if (i == 0)
    left = nums2[j - 1];
else if (j == 0)
    return (double) (nums1[i - 1] + nums2[j]) / 2.0;
else
    left = Math.max(nums1[i - 1], nums2[j - 1]);
if ((len1 + len2) % 2 == 1)
    return left;
if (i == len1)
    right = nums2[j];
else if (j == len2)
    right = nums1[i];
else
    right = Math.min(nums1[i], nums2[j]);
return (double) (left + right) / 2.0;

        将上述代码整合后可以得到解答：

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        if (nums1.length > nums2.length) return findMedianSortedArrays(nums2, nums1);
        int len1 = nums1.length,
            len2 = nums2.length,
            halfLen = (len1 + len2 + 1) / 2,
            iMin = 0,
            iMax = len1,
            i = 0,
            j = 0;

        while(iMin <= iMax) {
            i = (iMin + iMax) / 2;
            j = halfLen - i;
            if (i > 0 && j < len2 && nums1[i - 1] > nums2[j])
                iMax = i - 1;
            else if (j > 0 && i < len1 && nums2[j - 1] > nums1[i])
                iMin = i + 1;
            else
                break;
        }

        int left = 0, right = 0;
        if (i == 0)
            left = nums2[j - 1];
        else if (j == 0)
            return (double) (nums1[i - 1] + nums2[j]) / 2.0;
        else
            left = Math.max(nums1[i - 1], nums2[j - 1]);
        if ((len1 + len2) % 2 == 1)
            return left;
        if (i == len1)
            right = nums2[j];
        else if (j == len2)
            right = nums1[i];
        else
            right = Math.min(nums1[i], nums2[j]);
        return (double) (left + right) / 2.0;
    }
}

        时间复杂度为 $O(log(Min(nums1.length,\ nums2.length)))$ ，因为二分搜索为对数级复杂度，而在这道题中当我们在 $nums1[\ ]$ 中搜索到正确的 $i$ 时，也就意味着得到了 $j$ ，因此只需取两个数组之中最短的长度即可。空间复杂度为 $O(1)$ 。

回到顶部